基于GiveMeSomeCredit的贷款申请评分卡建模报告
建模背景
贷款申请评分卡是一种成熟的应用统计模型,其作用是对申请人做风险评估,识别可能产生逾期的客户并做出决策,包括申请审批和风险定价等,具有较高的准确性和可靠性。
本报告数据来源于GiveMeSomeCredit,通过介绍评分卡典型建模流程,希望读者能够就贷款申请评分模型有了初步了解。
算法选择说明
在贷款申请评分卡建模过程中,通常选择逻辑回归(Logistics Regression)算法,该算法的函数作用是将申请人的贷款申请信息综合起来并转化为逾期概率,为决策人员提供了量化风险评估的依据。
决策人员的风险评估思路如下:
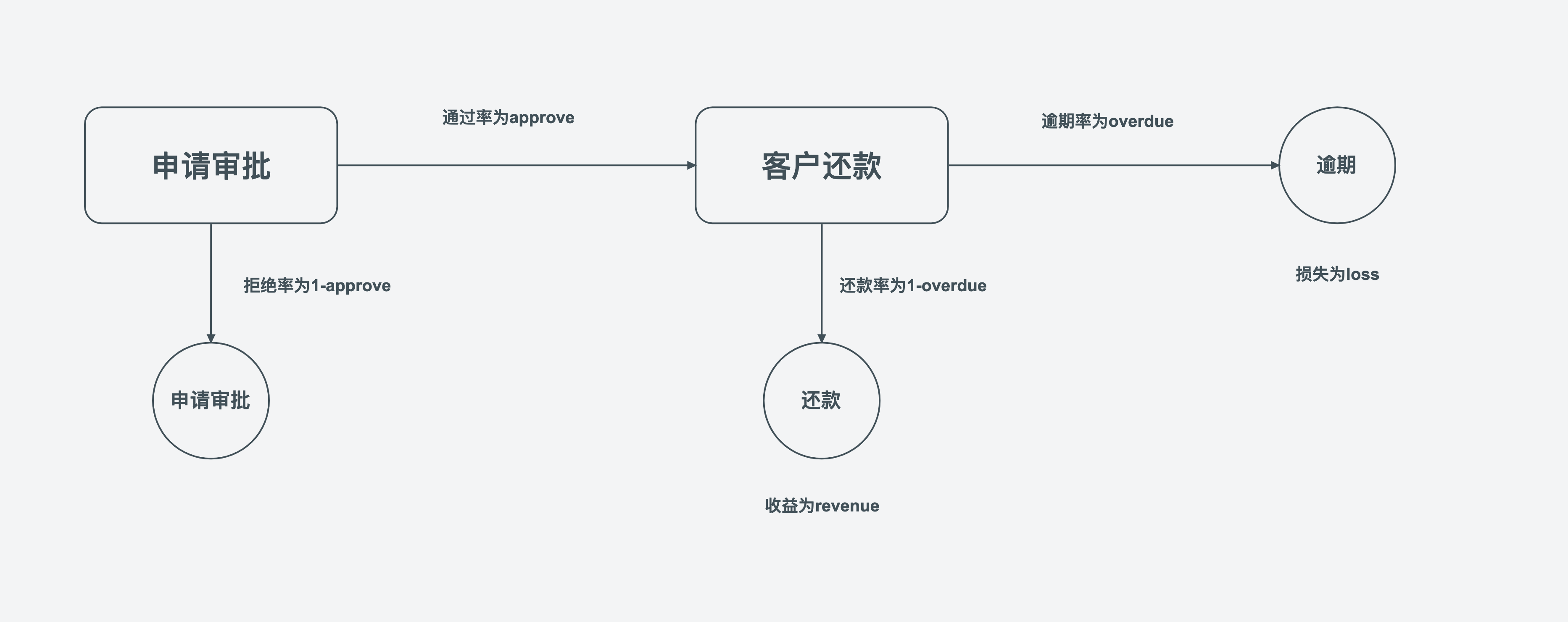
审批贷款申请时,假设只有通过或拒绝两种审批结果,审批通过的概率为\(approve\)。审批通过后,客户也只有还款或逾期两种还款结果,逾期的概率为\(overdue\)(还款的概率为\(repay\),\(overdue+repay=1\))。银行就逾期的损失为\(loss\),就还款的收益为\(revenue\)。综合收益为:
\[approve(repay\times revenue-overdue\times loss)\]站在决策人员的立场,审批通过的充分条件为综合收益大于零,推导可得:
\[overdue / repay < revenue / loss\]就是说,当该申请人发生逾期的概率和还款的概率的比值(定义为逾期还款概率比率,\(odd\))小于收益和损失的比值审批通过。所以,计算申请人的逾期还款概率比率成为首要工作。
假设,已知申请人的贷款申请信息(定义为特征变量的值的集合,\(x=({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m)})\)),则该申请人的逾期还款概率比率为:
\[odd(overdue|({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m}))=p(overdue|({x}_{1,}{x}_{2},\cdot \cdot \cdot {x}_{m}))/p(repay|({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m}))\] \[=p(overdue)/p(repay)\times (f({x}_{1,}{x}_{2},\cdot \cdot \cdot {x}_{m}|overdue)/f({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m}|repay))\] \[=p(overdue)/p(repay)\times f({x}_{1}|overdue)/f({x}_{1}|repay)\times f({x}_{2}|overdue)/f({x}_{2}|repay)\times \cdot \cdot \cdot f({x}_{m}|overdue)/f({x}_{m}|repay)\] \[\to F(x)=ln(odd(overdue|({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m})))\] \[=ln(p(overdue)/p(repay))+ln(f({x}_{1}|overdue)/f({x}_{1}|repay))+\cdot \cdot \cdot ln(f({x}_{m}|overdue)/f({x}_{m}|repay))\]定义\(ln(f({x}_{i}|overdue)/f({x}_{i}|repay))\)为特征变量的值的的证据权重\(woe({x}_{i})\),就数据集而言证据权重是评价某个特征变量逾期还款分布情况的较好统计量。
综上所述,在每个特征变量相互独立的情况下,计算申请人的逾期还款概率比率为对数逾期还款样本比率加上各特征变量的值的证据权重,即\(F(x)=a+\sum ^{m}_{i=1} {woe({x}_{i})}\)。
另外,推导可得:
\[odd(overdue|F({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m})=F(x))={e}^{F(x)}\] \[=p(overdue|({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m}))/p(repay|({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m}))\] \(\to p(overdue|({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m}))=1/(1+{e}^{-F(x)})\),刚好是逻辑回归函数!将\(F(x)\)由对数比率经线性转化则为贷款申请评分卡!
建模流程
获取数据
连接数据库获取原始数据集,目标变量为SeriousDlqin2yrs,特征变量数为10个。数据预览如下:
数据预处理
数据清洗
删除目标变量包含缺失值和重复的样本。处理后,样本数为{{samples}}份。
缺失值处理
在特征变量证据权重编码时,将对缺失值单独作为一箱并纳入模型。
异常值处理
在特征变量证据权重编码时,可消除异常值的影响,故不作异常值处理。
特征变量证据权重编码
逻辑回归假设之一为特征变量和目标变量之间存在线性关系,但在实际情况多为非线性。通过分箱,可将非线性关系转化为线性。另外,分箱可以减少缺失值和异常值对逻辑回归的影响并提升逻辑回归的鲁棒性。
本次报告使用决策树进行分箱,分箱后使用证据权重编码。以特征变量“Age”为例,其证据权重编码结果如下:
由上图可看出,特征变量“Age”分箱后各箱证据权重呈线性关系且单调递减,即随着年龄升高逾期还款概率比率降低。这与贷款申请审批经验符合,其经济稳定性的增强、收入水平的提升、信用记录的积累、消费观念的成熟以及风险管理能力的提升,表现出更低的逾期风险。
决策树分箱说明
- 统计特征变量值数,取其与5的最小值作为决策树算法的最大叶节点数(本次报告控制最大分箱数为5,最小叶节点样本数为5%)。
- 基于最大叶节点数使用决策树算法就特征变量拟合目标变量,利用决策树的分裂节点作为划分点进而将连续型特征变量划分为不同的区间。
- 统计各区间的证据权重并检验单调性。
- 如果检验通过,则将上述区间作为特征变量分箱结果。如果检验未通过,则将最大叶节点数减1并重复上述步骤至检验通过。
特征变量选择
基于信息价值选择特征变量
信息价值是与证据权重密切相关的指标,可用来评估特征变量的预测能力。通常,选择信息价值大于等于0.1的特征变量。
\[iv=(overduty-repay)\times ln(odd)\]信息价值说明
概率是描述随机变量确定性的量度,熵是描述随机变量不确定性的量度。假设\(p(x)\)和\(q(x)\)是逾期和还款的两个概率分布,可使用相对熵表示\(q(x)\)拟合\(p(x)\)所产生的信息损失,公式如下:
\[D(p||q)=\sum {p(x)log(p(x)/q(x))}\]相对熵没有对称性,即\(D(p||q)\neq D(q||p)\),如果将两个概率分布之间的相对熵求和,和越大说明两个概率分布的距离越大。该和即为KL距离,公式如下:
\[DistanceKL=\int {(f(p|overduty)-f(p|repay))\times log(f(p|overduty)/f(p|overduty))dx}\]上式离散形式即为信息价值。在选择特征变量时,特征变量的信息价值越大说明逾期还款的概率分布的距离越大、区分逾期还款的能力越强。
基于有条件的后向步进淘汰特征变量
使用逻辑回归算法需检验其前提条件:
- 特征变量之间相互独立
- 特征变量的回归系数均为正数
本次报告使用方差扩大因子(Variance Inflation Factor)评估特征变量与其它变量的共线性。通常,淘汰方差扩大因子大于5的特征变量。
\[vif=1/(1-{maximun(r)}^{2})\]其中,\(r\)为特征变量与其它特征变量的复相关系数。
有条件的后向步进淘汰特征变量说明
- 统计特征变量的方差扩大因子和回归系数。
- 淘汰方差扩大因子大于5或回归系数小于0.1且方差扩子因子最大的特征特征变量。
- 重复上述步骤至没有特征变量可淘汰。
处理后,选择的特征变量数为{{variables_independent}}个,特征变量预览如下:
评分卡开发和验证
评分卡开发
本次报告中贷款申请评分卡公式为(本次报告控制\(a\)为500,\(b\)为\(50/ln(2)\)):
\[score=a-blog(odd(overdue|({x}_{1},{x}_{2},\cdot \cdot \cdot {x}_{m})))\] \[=a-b({\beta }_{0}+{\beta }_{1}woe({x}_{1})+{\beta }_{2}woe({x}_{2})+\cdot \cdot \cdot {\beta }_{m}woe({x}_{m}))\]其中,\({\beta }_{i}\)为特征变量的回归系数(\({\beta }_{0}\)基于回归系数分摊至各特征变量)。
以“Age”为例,其评分卡编制结果如下:
由上表可看出,\(分数=加权基础分数+加权回归系数\times 证据权重\)。
评分卡验证
本次报告使用柯斯和提升统计量评估评分卡,柯斯统计量为{{ks}},提升统计量为{{lift}}。
柯斯统计量说明
柯斯统计量全称Kolmogorov-Smirnov,常用于评估模型对于目标变量的区分能力。先将总分数划分为若干区间并作为横坐标,再将逾期和还款的累计样本数占比作为纵坐标,即可绘制两条洛伦兹曲线。柯斯统计量就是两条洛伦兹曲线间最大距离。
通常,柯斯统计量小于20不建议使用该评分卡,20~40说明该评分卡区分能力较好、40~50良好、50~60很好、60~75非常好,大于75建议审慎使用。
提升统计量说明
提升统计量,常用于量化评估模型对目标变量的预测能力较随机选择的提升程度。先将总分数划分为若干区间并作为横坐标,再计算各区间的累计逾期样本数占比和累计样本数占比的比值,最大值就是提升统计量。
通常,提升统计量折线图在高位保持若干区间后迅速下降至1时,表示该评分卡区分能力较好。
评分卡评价表
以分箱[500, 550)为例,该分箱5.61%是逾期客户。假设,审批通过16位客户产生的收益可平衡1位逾期客户的损失,5.61%可作为平衡点,拒绝规则不能低于550,否则损失大于收益。
以拒绝规则<550为例,若选择该拒绝规则,则会拒绝36.53%客户,这部分中15.72%是逾期客户。使用该评分卡后,逾期客户减少85.59%。